MOVIMIENTO OSCILATORIO
En el movimiento periódico el objeto regresa regularmente a una posición conocida después de un intervalo de tiempo fijo.
Movimiento de un objeto unido a un resorte
Como un modelo de movimiento armónico simple considere un bloque de masa m unido al extremo de un resorte, con el bloque libre de moverse sobre una superficie horizontal sin fricción. Cuando el resorte no está estirado ni comprimido, el bloque queda en reposo, es decir en la posición de equilibrio del sistema que se puede identificar porque x = 0.
Si el bloque se desplaza a una posición x el resorte ejerce sobre el bloque una fuerza que es proporcional a la posición y se conoce como Ley de Hooke.
Donde Fs es la fuerza restauradora que está dirigida en sentido contrario del desplazamiento, k es una constante y x es la posición del bloque.
Al aplicar la segunda ley de Newton en la formula anterior tenemos que:
Es decir, la aceleración del bloque es proporcional a su posición, y la dirección de la aceleración es opuesta a la dirección del desplazamiento del bloque desde el equilibrio. Se dice que los sistemas que se comportan de esta forma exhiben movimiento armónico simple. Un objeto se mueve con movimiento armónico simple siempre que su aceleración es proporcional a su posición y se dirige en sentido opuesto al desplazamiento desde el equilibrio.
PARTICULA EN MOVIMIENTO ARMONICO SIMPLE
Para el estudio de la partícula en movimiento armónico simple se considerara que se encuentra en condiciones perfectas, es decir que no se considerara la fricción del objeto con el suelo.
Recuerde que, por definición, a =dv/dt = d 2x/dt2 , por lo tanto la ecuación 2 quedaría
Reemplazando ⍵2 en la fórmula 3 tendríamos:
Aplicando integrales la ecuación 4 quedaría:
Donde A, ⍵ y ф son constantes.
PERIODO
El periodo T del movimiento es el intervalo de tiempo requerido para que la partícula pase atreves de un ciclo
<!--[endif]-->FRECUENCIA:
Numero de oscilaciones que experimenta la partícula por unida de intervalo de tiempo
Ecuación para calcular la velocidad en función del tiempo
Donde el valor más alto de sen es +- 1, por lo tanto el valor máximo de la velocidad seria
Ecuación para calcular la aceleración en función del tiempo
Donde el valor más alto del cos es +-1, por lo tanto el valor máximo de la aceleración es:
ENERGIA DEL OSCILADOR ARMONICO SIMPLE
La energía mecánica del sistema bloque-resorte siempre va hacer la misma.
<!--[if !supportLists]-->· <!--[endif]-->Energía cinética:
La energía cinética del sistema solo corresponde a la del bloque se puede utilizar la ecuación 8 para expresar la energía cinética del bloque, quedaría de la siguiente forma.
<!--[if !supportLists]-->· <!--[endif]-->Energía potencial:
La energía potencial elástica almacenada en el resorte para cualquier elongación x se conoce por 1/2kx2
La energía mecánica total seria:
La energía mecánica total de un oscilador es una constante k y la amplitud al cuadrado.








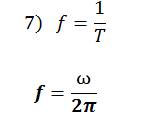




No hay comentarios:
Publicar un comentario