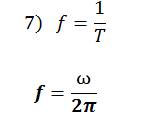FÍSICA II

MOVIMIENTO OSCILATORIO

En el movimiento periódico el objeto regresa regularmente a una posición conocida después de un intervalo de tiempo fijo.

Movimiento de un objeto unido a un resorte

Como un modelo de movimiento armónico simple considere un bloque de masa m unido al extremo de un resorte, con el bloque libre de moverse sobre una superficie horizontal sin fricción. Cuando el resorte no está estirado ni comprimido, el bloque queda en reposo, es decir en la posición de equilibrio del sistema que se puede identificar porque x = 0.

Si el bloque se desplaza a una posición x el resorte ejerce sobre el bloque una fuerza que es proporcional a la posición y se conoce como Ley de Hooke.

Donde F_s es la fuerza restauradora que está dirigida en sentido contrario del desplazamiento, k es una constante y x es la posición del bloque.

Al aplicar la segunda ley de Newton en la formula anterior tenemos que:

Es decir, la aceleración del bloque es proporcional a su posición, y la dirección de la aceleración es opuesta a la dirección del desplazamiento del bloque desde el equilibrio. Se dice que los sistemas que se comportan de esta forma exhiben movimiento armónico simple. Un objeto se mueve con movimiento armónico simple siempre que su aceleración es proporcional a su posición y se dirige en sentido opuesto al desplazamiento desde el equilibrio.

Ejemplos:

PARTICULA EN MOVIMIENTO ARMONICO SIMPLE

Para el estudio de la partícula en movimiento armónico simple se considerara que se encuentra en condiciones perfectas, es decir que no se considerara la fricción del objeto con el suelo.

Recuerde que, por definición, a =dv/dt = d ²x/dt², por lo tanto la ecuación 2 quedaría

Reemplazando ⍵² en la fórmula 3 tendríamos:

Aplicando integrales la ecuación 4 quedaría:

Donde A, ⍵ y ф son constantes.

PERIODO

El periodo T del movimiento es el intervalo de tiempo requerido para que la partícula pase atreves de un ciclo

FRECUENCIA:

Numero de oscilaciones que experimenta la partícula por unida de intervalo de tiempo

Ecuación para calcular la velocidad en función del tiempo

Donde el valor más alto de sen es +- 1, por lo tanto el valor máximo de la velocidad seria

Ecuación para calcular la aceleración en función del tiempo

Donde el valor más alto del cos es +-1, por lo tanto el valor máximo de la aceleración es:

ENERGIA DEL OSCILADOR ARMONICO SIMPLE

La energía mecánica del sistema bloque-resorte siempre va hacer la misma.

· Energía cinética:

La energía cinética del sistema solo corresponde a la del bloque se puede utilizar la ecuación 8 para expresar la energía cinética del bloque, quedaría de la siguiente forma.

· Energía potencial:

La energía potencial elástica almacenada en el resorte para cualquier elongación x se conoce por 1/2kx²

La energía mecánica total seria:

La energía mecánica total de un oscilador es una constante k y la amplitud al cuadrado.

FÍSICA

Lunes, 27 de mayo del 2013

Ondas Sonoras

Introducción:

Las ondas sonoras viajan a través de cualquier medio material con una rapidez que depende de las propiedades del medio. A medida que las ondas sonoras viajan a través del aire, los elementos del aire vibran para producir cambios en densidad y presión a lo largo de la dirección del movimiento de la onda. Si la fuente de las ondas sonoras vibra sinusoidalmente, las variaciones de presion también son sinusoidales. La descripción matemática de las ondas sonoras sinusoidales es muy parecida a las ondas sinusoidales en cuerdas, que se explicaron en el capitulo 16.

Las ondas sonoras se dividen en tres categorías que cubren diferentes intervalos de frecuencia.

1) Las ondas audibles se encuentran dentro del intervalo de sensibilidad del oído humano. Es posible generarlas en una variedad de formas, como de instrumentos musicales, voces humanas o bocinas.

2) Las ondas infrasónicas tienen frecuencias por abajo del intervalo audible. Los elefantes usan ondas infrasonicas para comunicarse mutuamente, aun cuando estén separados por varios kilómetros.

3) Las ondas ultrasónicas tienen frecuencias por arriba del alcance audible. Es posible que usted haya usado silbatos “silenciosos” para llamar a su perro. Los perros escuchan el sonido ultrasonico que emite este silbato, para los humanos es imposible detectarlo. Las ondas ultrasónicas también se usan para la

formación de imagen médica.

Rapidez de Ondas Sonoras:
La rapidez de las ondas en un medio depende de la compresibilidad y de la desnidad del medio; si éste es un líquido o un gas y tiene un módulo volumétrico B y densidad "p", la rapidez de ls ondas sonoras en dicho medio es de: velocidad es igual a la raíz cuadrada de el módulo volumétrico "B" entre la densidad.

Para ondas longitudinales en una barra sólida de material la rapidez depende del módulo de Young "Y" y de la densidad "p".

La rapidez del sonido depende del tipo de material en el que se encuentra. En la siguiente tabla se muestra la rapidez del sonido en distintos tipos de materiales.

Ondas Sonoras Periódicas

Uno puede producir una onda sonora periódica unidimensional mediante un émbolo vibratorio en un extremo de un tubo largo y estrecho que contenga gas. Las regiones más oscuras de la figura representan regiones donde el gas se comprime, por lo que en ellas la densidad y la presión están arriba de sus valores de equilibrio.

Región comprimida

Se forma cada vez que el émbolo se empuja hacia adentro del tubo.

Condensación

Región comprimida que se mueve por el tubo como un pulso, y comprime continuamente las capas enfrente de ella.

Rarefacciones

Se propagan también a lo largo del tubo, siguiendo a las condensaciones. Las dos regiones se mueven con una velocidad igual a la del sonido en ese medio (aproximadamente 343 m/s en el aire a 20o C).
La distancia entre dos condensaciones sucesivas es igual a la longitud de onda.

Si s(x,t) es el desplazamiento de un `pequeño elemento de volumen medido a partir de su posición de equilibrio, podemos expresar esta función de desplazamiento armónico como

s(x,t) = smáx cos (x -t)

donde smax es el desplazamiento máximo del medio a partir del equilibrio (en otras palabras, la amplitud de desplazamiento, es el número de onda angular, y es la frecuencia angular del émbolo, el desplazamiento del medio es a lo largo de x.

La variación en la presión del gas, "P, medida desde su valor de equilibrio, también es periódica y está dada por

"P = "Pmáx sen(x -t)

La amplitud de presión "Pmax es el cambio máximo en la presión a partir de su valor de equilibrio, la amplitud d presión es proporcional a la amplitud de desplazamiento, smax:

Amplitud de presión "Pmáx = smáx

donde smax es la velocidad longitudinal máxima del medio frente al émbolo.

Una onda longitudinal senoidal se propaga por un tubo lleno con un gas compresible. La fuente de la onda es un émbolo vibrante a la izquierda. Las regiones de alta y baja presión son oscuras y claras, respectivamente.

· Amplitud de desplazamiento contra posición, y

· Amplitud de presión contra posición de una onda longitudinal senoidal.

La onda de desplazamiento está 90ofuera de fase respecto de la onda de presión.

A partir de la definición de módulo volumétrico vemos que la variación de presión en un gas es:

"P = - B

El volumen de un segmento del medio que tiene un espesor "x en la dirección horizontal y un área de sección transversal A es V = A"x. El cambio en el volumen "V que acompaña al cambio de presión es igual a A"s, donde "s es la diferencia entre el valor de s en x + "x y el valor de s en x. Por tanto, podemos expresar "P como:

"P = - B = - B = - B

A medida que "x se aproxima a cero, la proporción "s/"x se vuelve "s/"x. (En este caso empleamos la derivada parcial para indicar que estamos interesados en la variación de s con la posición en un tiempo fijo.) En consecuencia,

"P = - B

Si el desplazamiento es la función senoidal simple dada por la ecuación anterior encontramos que se va reduciendo y sustituyendo hasta quedarnos la ecuación.

"P = "Pmáx sen (x -t)

Miercoles, 29 de mayo del 2013

Intensidad de ondas sonoras periódicas

Considere una capa de aire de masa "n y ancho "x enfrente de un émbolo que oscila con una frecuencia angular , como en la figura.

Un émbolo oscilante transfiere energía al gas en el tubo, con lo cual hace que la capa de ancho "x y la masa "m oscile con amplitud smáx.

Émbolo

Transmite energía a la capa de aire. Puesto que la energía cinética promedio es igual a la energía potencial promedio en un movimiento armónico simple, la energía total promedio de la masa "m es igual a su energía cinética máxima.

Energía promedio de la capa de aire en movimiento

"E = ½ "m (smáx)2 = ½ ("x) (smáx)2

donde A "x es el volumen de la capa. La tasa en el tiempo a la cual se transfiere la energía a cada capa. La potencia es:

Potencia = = ½ A (smáx)2 = ½ A(smáx)2

Donde v = "x/"t es la velocidad de la perturbación hacia la derecha.

Intensidad I de una onda

Potencia por unidad de área, como la tasa a la cual la energía que es transportada por la onda fluye por un área unitaria A perpendicular a la dirección de propagación de la onda.

La intensidad es:

Potencia

I = área = ½ (smáx)2

Así, vemos que la intensidad de una onda sonora periódica es proporcional al cuadrado de la amplitud y al cuadrado de la frecuencia. Esto también puede escribirse en función de la amplitud de presión "Pmáx, utilizando la ecuación anterior lo cual produce.

Niveles sonoros en decibeles

Nivel sonoro se define mediante la ecuación

"10 log

La constante I0 es la intensidad de referencia, considerada como umbral auditivo ( I0 = 1.00 x 10-12 W/m2), e I es la intensidad en watts por metro cuadrado en el nivel sonoro , donde se mide en decibeles (dB).2

La exposición prolongada a intensos niveles sonoros puede producir un daño serio al oído. Es recomendable utilizar tapones en los oídos siempre que los niveles sonoros sean mayores a 90 dB.

Se dice que la “contaminación por ruido” puede ser un factor que contribuye a la alta presión sanguínea, la ansiedad y el nerviosismo.

La siguiente tabla brinda algunos valores característicos de los niveles sonoros de diferentes fuentes.

El efecto Doppler

Un ejemplo del efecto doppler es cuando un auto o camión se mueve mientras hace sonar su bocina, la frecuencia del sonido que se escucha es más alta a medida que el vehículo se acerca a usted y más baja cuando se aleja.

Se experimente un efecto doppler siempre que hay un movimiento relativo entre la fuente y el observador. Cuando la fuente y el observador se mueven uno hacia el otro la frecuencia que escucha el observador es más alta que la frecuencia de la fuente. Cuando la fuente y el observador es más baja que la frecuencia de la fuente.

El efecto doppler se utiliza en sistemas de radar de la policía para medir la velocidad de vehículos automotores. De manera similar, los astrónomos aprovechan este efecto para determinar el movimiento relativo de estrellas, galaxias y otros objetos celestes.

Un observador O que se mueve con una velocidad v0 hacia una fuente puntual estacionaria S escucha una frecuencia que es mayor que la frecuencia de la fuente.

Consideremos la frecuencia de la fuente igual a , la longitud de onda.

Donde el signo positivo se emplea cuando el observador se mueve hacia la fuente, y el signo negativo se mantiene cuando el observador se aleja de la fuente.

Durante cada vibración, que dura un tiempo T (el período), la fuente se mueve a una distancia

sT = s/ y la longitud de la onda se acorta en esta cantidad.

La palabra hacia se asocia con un aumento en la frecuencia observada. Las palabras alejándose de se asocian con una disminución en la frecuencia observada.

Una fuente S se mueve con una velocidad s hacia un observador estacionario A y se aleja de un observador estacionario B. El observador A escucha una frecuencia creciente, y el observador B escucha una frecuencia que se reduce.

Una representación de una onda de choque producida cuando una fuente se mueve de S0 a Sn con una velocidad s la cual es más grande que la velocidad de onda en ese medio. La envolvente de los frentes de onda forma un cono cuyo ápice de medio ángulo está dado por sen = 1/s.

Ejercicios [Propuestos]:

- 1) Enunciado: Encuentre la rapidez del sonido a través del mercurio, que tiene un modulo volumétrico de 2.80 x 10¹⁰ N/m2 y una densidad de 13 600 kg/m3.

Datos:

V = ?

d = 13600 kg/m³

Resolución:

- 2) Enunciado: Un delfín en agua de mar, a una temperatura de 25°C, da un chirrido. ¿Cuanto tiempo pasa antes de que escuche un eco desde el fondo del océano, 150 m abajo?

Datos:

T = 25°C

x = 150m

Resolución:

El pulso de sonido debe viajar 150 m antes y 150 m después de la reflexión. Tenemos entonces que d = vt

- 3) Enunciado: El ultrasonido se usa en medicina tanto para formacion de imagen diagnostica como para terapia. Para diagnosis: pulsos cortos de ultrasonido pasan a traves del cuerpo del paciente, se registra un eco reflejado de una estructura de interes y es posible determinar la distancia a la estructura a partir del retraso de tiempo para que regrese el eco. Un solo transductor emite y detecta el ultrasonido. Al reducir los datos con una computadora se obtiene una imagen de la estructura. Con sonido de baja intensidad, esta tecnica no es invasiva y es inocua: se usa para examinar fetos, tumores, aneurismas, calculos y muchas otras estructuras. Para revelar detalles, la longitud de onda del ultrasonido reflejado debe ser pequena comparada con el tamano del objeto que refleja la onda. a) ¿Cual es la longitud de onda del ultrasonido con una frecuencia de 2.40 MHz que se usa en ecocardiografia para mapear el latido del corazón humano? b) En todo el conjunto de tecnicas de formacion de imagen se usan frecuencias en el intervalo de 1.00 a 20.0 MHz. ¿Cual es el intervalo de longitudes de onda que corresponden a este intervalo de frecuencias? La rapidez del ultrasonido en el tejido humano es de aproximadamente 1 500 m/s (casi la misma que la rapidez del sonido en el agua).

Resolución:

a) Si F = 2.4 MHz