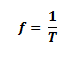FÍSICA II: mayo 2013

EJERCICIOS EN CLASE

Un oscilador armónico simple tarda 12.0 s en someterse a cinco vibraciones completas. Encuentre a) el periodo de su movimiento, b) la frecuencia en hertz y c) la frecuencia angular en radianes por segundo.

Un bloque de 200 g se une a un resorte horizontal y ejecuta movimiento armónico simple con un periodo de 0.250 s. La energía total del sistema es de 2.00 J. Encuentre a) la constante de fuerza del resorte y b) la amplitud del movimiento.

Un sistema bloque–resorte oscila con una amplitud de 3.50 cm. La constante de resorte es 250 N/m y la masa del bloque es 0.500 kg. Determine a) la energía mecánica del sistema, b) la rapidez máxima del bloque y c) la aceleración máxima.

Un objeto de 2.00 kg se une a un resorte y se coloca sobre una superficie horizontal uniforme. Se requiere una fuerza horizontal de 20.0 N para mantener al objeto en reposo cuando se jala 0.200 m desde su posición de equilibrio (el origen del eje x). Ahora el objeto se libera desde el reposo con una posición inicial xi 􀀕 0.200 m y se somete a sucesivas oscilaciones armónicas simples. Encuentre a) la constante de fuerza del resorte,

b) la frecuencia de las oscilaciones y c) la rapidez máxima del objeto. ¿Dónde se presenta la rapidez máxima? d) Encuentre la aceleración máxima del objeto. ¿Dónde se presenta? e) Encuentre la energía total del sistema oscilante. Encuentre f) la rapidez y g) la aceleración del objeto cuando su posición es igual a un tercio del valor máximo.

Un objeto de 1.00 kg se une a un resorte horizontal. El resorte inicialmente se estira 0.100 m y ahí se libera el objeto desde el reposo. Éste comienza a moverse sin fricción. La siguiente vez que la rapidez del objeto es cero es 0.500 s después. ¿Cuál es la rapidez máxima del objeto?

Un objeto de 50.0 g, conectado a un resorte con una constante de fuerza de 35.0 N/m, oscila sobre una superficie horizontal sin fricción con una amplitud de 4.00 cm. Encuentre a) la energía total del sistema y b) la rapidez del objeto cuando la posición es de 1.00 cm. Encuentre c) la energía cinética y d) la energía potencial cuando la posición es de 3.00 cm.

EL PÉNDULO

El péndulo de Foucault en el Instituto Franklin de Filadelfia. Este tipo de péndulo fue utilizado por primera vez por el físico francés Jean Foucault para verificar la rotación de la Tierra experimentalmente.

Como las oscilaciones del péndulo, el plano vertical en el que oscila parece rotar, golpea sucesivamente sobre los indicadores dispuestos en un círculo en el suelo. En realidad, el plano de oscilación se fija en el espacio y la Tierra que gira bajo el péndulo se mueve en los indicadores condiciones de ser derribado, una tras otra.

El péndulo simple es otro sistema mecánico que muestra movimiento periódico. Consiste en una plomada parecida a una partícula de masa m suspendida de una cuerda ligera de longitud L que está fija en el extremo superior.

Las fuerzas que actúan en la plomada son la fuerza T que ejerce la cuerda y la fuerza gravitacional m.

La ecuación del movimiento tangencial, compuesta por la fuerza restauradora se puede describir en función del desplazamiento.

Se puede usar la aproximación de ángulo pequeño, en la que sen Ø = Ø, donde Ø se mide en radianes.

En tanto Ø sea menor que 10°, el ángulo en radianes y su seno son los mismos aproximadamente.

_{LABORATORIO DE FÍSICA 2}

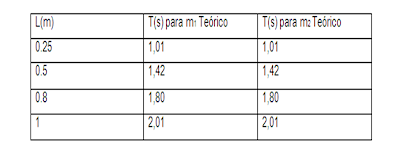
Diseñar 2 péndulos con diferentes masas m1 y m2 registrar el periodo de oscilación en la siguiente tabla, el angulo de oscilación debe ser inferior debe ser inferior a 10%.

Formula: T= 2π/W

Calcule el periodo de oscilación utilizando la fuerza de la gravedad igual a 9.7799 m/s2.

Calcular el porcentaje de error exp en cada caso, utilice la fórmula:

Cuál será el periodo de oscilación del péndulo con la masa m1, si se lo lleva uno de los polos, la gravedad en los polos es 9.83 m/s²

MOVIMIENTO ONDULATORIO

El mundo está lleno de ondas, los dos tipos principales son las ondas mecánicas y las ondas electromagnéticas. En el caso de las ondas mecánicas, algunos medios físicos se perturban; en el ejemplo de la piedra, los elementos del agua se perturban.

Las ondas electromagnéticas no requieren un medio para propagarse; algunos ejemplos de ondas electromagnéticas son la luz visible, las ondas de radio, las señales de televisión y los rayos X. La característica central del movimiento ondulatorio es que la energía se transfiere a través de una distancia, pero la materia no.

Todas las ondas mecánicas requieren:

Alguna perturbación.
Un medio que contenga elementos que sean factibles de perturbación.
Algún mecanismo físico a partir del cual los elementos del medio puedan influirse mutuamente

La cuerda es el medio a través del cual viaja el pulso; éste alcanza una altura y una rapidez de propagación definidas a lo largo del medio (la cuerda).

La forma del pulso cambia muy poco a medida que viaja a lo largo de la cuerda. Una onda viajera o pulso que hace que los elementos del medio perturbado se muevan perpendiculares a la dirección de Una onda viajera o pulso que hace que los elementos del medio perturbado se muevan perpendiculares a la dirección de propagación se llama onda transversal. Compare esta onda con otro tipo de pulso, uno que se mueve por un largo resorte estirado.

El extremo izquierdo del resorte recibe un ligero empuje hacia la derecha y después recibe un ligero jalón hacia la izquierda. Este movimiento crea una súbita compresión de una región de las espiras. Observe que la dirección del desplazamiento de las espiras es paralela a la dirección de propagación de la región comprimida.

Una onda viajera o pulso que mueve a los elementos del medio en paralelo a la dirección de propagación se llama onda longitudinal. Las ondas tridimensionales que viajan desde un punto abajo de la superficie de la Tierra donde se presenta un terremoto, son de ambos tipos, transversales y longitudinales. Las ondas longitudinales (Ondas P) viajan en la superficie terrestre entre 7 a 8 Km/s. Las ondas transversales (Ondas S) viajan en la superficie terrestre entre 4 a 5 Km/s Al registrar en un sismógrafo el intervalo de tiempo entre las llegadas de estos dos tipos de ondas, se determina la distancia desde el sismógrafo al punto de origen de las ondas. Las esferas imaginarias desde tres o más estaciones de monitoreo, ubicadas muy separadas unas de otras, se intersecan en una región de la Tierra, y esta región es donde se presentó el terremoto.

Se representa la posición transversal (y) para todas las posiciones y tiempos, medida en un marco estable con el origen en O, como:

Se aplica la ecuación (16.1) si el pulso viaja a la derecha. De igual modo, si el pulso viaja hacia la izquierda, las posiciones transversales de los elementos de la cuerda se describen mediante:

EL MODELO DE ONDA PROGRESIVA

La onda representada por esta curva se llama onda sinusoidal porque la curva es la misma que en la función sen (ɵ) trazada con ɵ. Una onda sinusoidal se podría establecer en una soga al agitar el extremo de la soga arriba y abajo en movimiento armónico simple. Enseguida se desarrollarán las características principales y representaciones matemáticas del modelo de análisis de una onda progresiva.

La distancia de una cresta a la siguiente se llama longitud de onda ʎ (letra griega lambda). La longitud de onda es la distancia mínima entre dos puntos cualesquiera en ondas adyacentes. El periodo es el intervalo de tiempo requerido para que dos puntos idénticos de ondas adyacentes pasen por un punto. El periodo de la onda es el mismo que el periodo de la oscilación armónica simple de un elemento del medio. La frecuencia de una onda periódica es el número de crestas que pasa un punto determinado en un intervalo de tiempo unitario. La frecuencia de una onda sinusoidal se relaciona con el periodo mediante la expresión:

La frecuencia de la onda es la misma que la frecuencia de la oscilación armónica simple de un elemento del medio. La unidad de frecuencia es el Hertz (Hz). La correspondiente unidad para T es segundos. La máxima posición de un elemento del medio relativo a su posición de equilibrio se llama amplitud A de la onda. Las ondas viajan con una rapidez específica, y esta rapidez depende de las propiedades del medio perturbado. Por ejemplo, las ondas sonoras viajan a través de aire a temperatura ambiente con una rapidez aproximada de 343 m/s, mientras que en la mayoría de los sólidos viajan con una rapidez mayor a 343 m/s. La función de la onda sinodal se puede expresar como:

donde a es una constante que se debe determinar.

En x = 0:

El siguiente valor de (x) para que (y) sea igual a cero es x= ʎ/2, entonces:

Considere la onda sinusoidal que se mueve a la derecha con una rapidez v, la función de onda en algún tiempo posterior t, se puede escribir como :

La función de onda tiene la forma f(x — vt). Si la onda viajara hacia la izquierda, la cantidad (x – vt) se sustituiría por (x + vt). Por definición, la onda viaja a través de un desplazamiento Δx igual a una longitud de onda ʎ en un intervalo de tiempo Δt de un periodo T. Por tanto, la rapidez de onda, la longitud de onda y el periodo se relacionan mediante la expresión.

La función de onda se expresa en una forma conveniente al definir otras dos cantidades, el número de onda angular k (por lo general simplemente llamado número de onda) y la frecuencia angular ω.